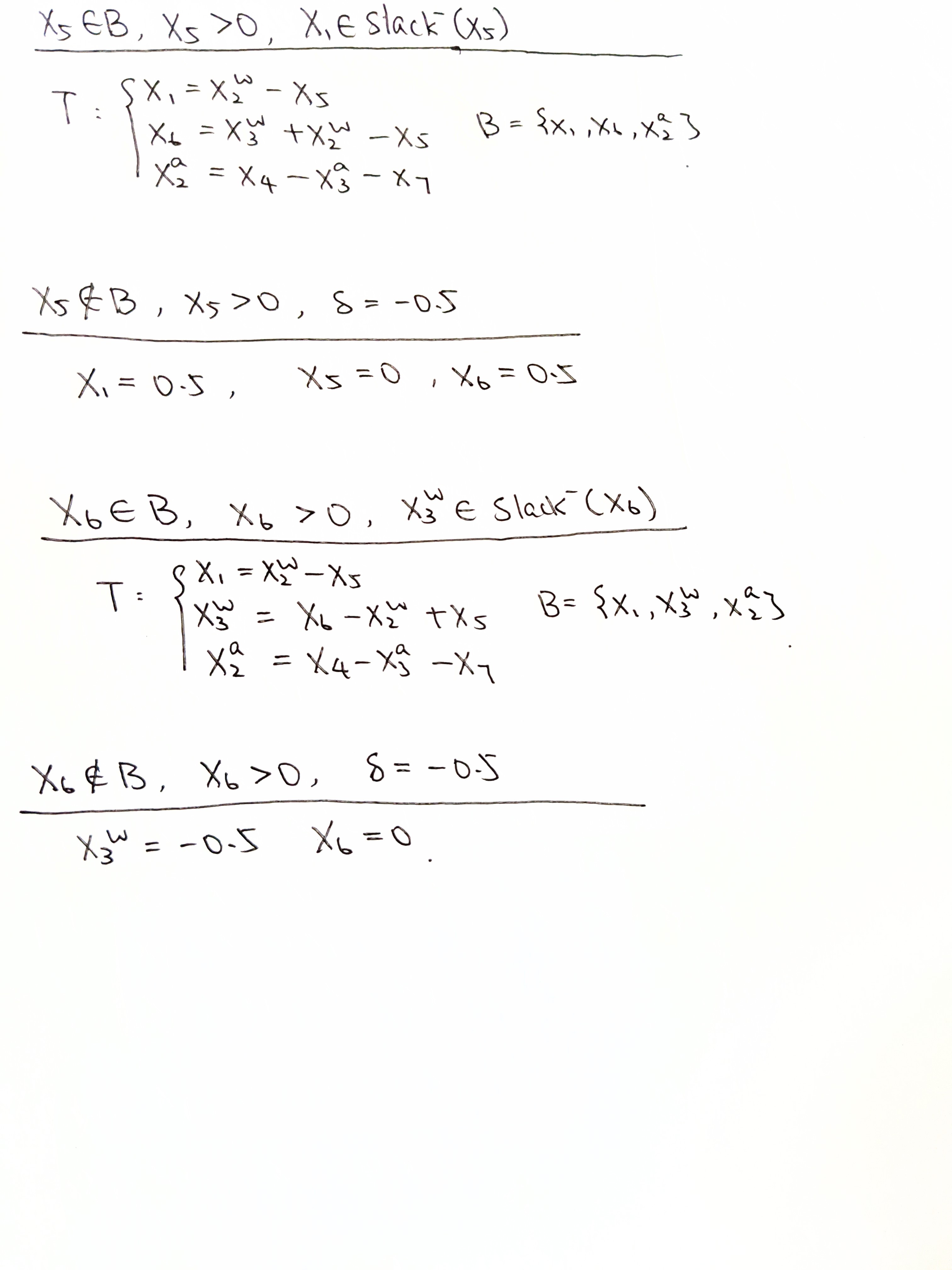Note on Neural Network Verification / Reluplex Paper
Problem to Solve
Given bound of input and output, whether the neural network model is satisfiable.
By directly applying existing solver on neural networks, the activation functions, which are encoded as disjunctions could lead to state explosion (suppose there are n activation function, solver has to explore $2^n$ states).
Background
Theory in SMT: A theory is $T = (\Sigma, I)$ where $\Sigma$ is called signature and $I$ is a list of closed interpretation. A $\tau$ is said to be $T$ satisfiable if it is satisfiable by $i \in I$.
DPLL(T): Embedding theories into DPLL algorithms (Details: https://www.cs.utexas.edu/~isil/cs389L/lecture16-6up.pdf)
Linear Real Arithmetic (LRA) Theory: $\Sigma = \{+,-,\cdot,\le, \ge,R\}$. And $\tau$ can be written as $\sum_{x_i} c_ix_i \square d$, $\square \in \{=,\le, \ge\}$.
ReLU: $ReLU(x) = max(0,x)$
Simplex for LRA: The Simplex algorithm proposed here is different from standard version. It is here for being a decision procedure for LRA theory. A configuration of can either be $<SAT, UNSAT>$ or $<\Beta, T, l,u,\alpha>$. $\Beta \sube X$ is called basic variables. $T$ is called tableau, which are a set of equations, $x_i = c_jx_j$, $x_i \in \Beta \wedge x_j \notin \Beta$. $x_j$ is known as non-basic variables. $l, u, \alpha$ are lower bound, upper bound, and real value assignment for each basic and non-basic variables.
Init: for each $\sum_{x_i} c_ix_i \square d$, make it $b =\sum_{x_i} c_i x_i$ where b is basic variable. Then $d$ is then applied to $l, u$. Make $\alpha$ with all zero.
Iteration:
Case 1 (A basic variable violates bound): a basic variable becomes non-basic and a non-basic becomes basic (update $\Beta$ and pivot corresponding equation in $T$) selected based on Slack rules (intuition: select a non-basic variable that can be changed in its bound such that could make the basic variable no longer violating its bound).
Case 2 (A non-basic variable violates bound): update $\alpha$ of the non-basic variable that violates the bound: $\alpha'(x_j) = \alpha(x_j) + \delta$ , where $x_j$ is the non-basic variable, and $a'(x_i) = a(x_i) + \delta T_{i,j}$ (intuition: the change on non-basic variable should be reflected on itself and propagate to all basic variables depending on it).
Termination: If no bound is violated, SAT. When there is no non-basic variable can be selected to exchange with the basic variable, UNSAT.
Implementation
Append R to configuration: $ReLU(x,y)\iff <x,y>\in R$.
Termination: Add check for ReLU constraints
Add ReLU pivoting
Add ReLU update
Add ReLU splitting. Only happens if # of other derivation rules applied to a ReLU exceeds a threshold. ~$ 30\%$ of ReLU has to be splitted for real-world examples if threshold is set to 5.
Simplex derivation rules:

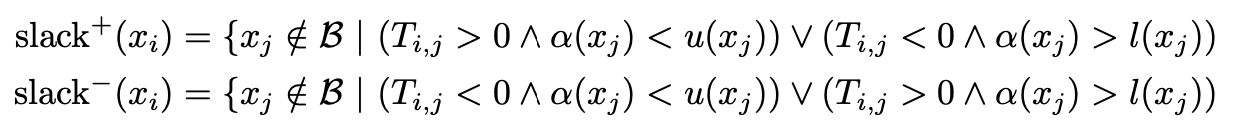
Reluplex new derivation rules for ReLU:
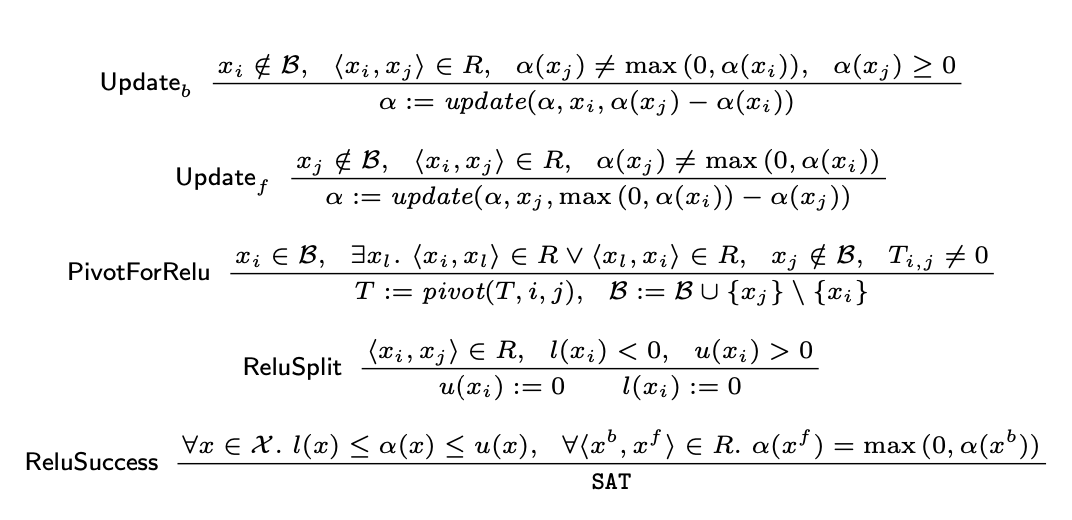
Optimization
Bound tightening
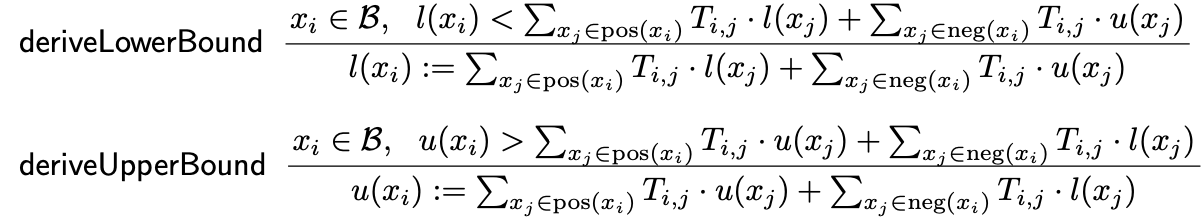
Conflict Analysis
Floating Point Arithmetic
- Measure the accumulated roundoff error after a certain number of pivot steps. Restore the coefficients of the current tableau T using the initial tableau $T_0$, if the error exceeded a threshold M.
Application
ACAS Xu Verification: ACAS Xu is the unmanned variant of Airborne Collision Avoidance System X. Previous certification methodologies included exhaustively testing the system in 1.5 million simulated encounters, but this is insufficient for proving that faulty behaviors do not exist within the continuous DNNs.
Adversarial attack: Let $\delta$ be the fluctuation. $||x - x'|| = \delta \implies \forall y_i, y_i^{'} \ge y_i$ , where $\xi^{'}$ signifies input and output after applying fluctuation. Intuitively, such a constraint asserts that for a threshold of fluctuation $\delta$ , the output would not be affected negatively. If this statement is valid, then the fluctuation applied would not affect the result, meaning that the adversarial attack has failed. With this in mind, we could then leverage the concept of binary search to find the maximal threshold of fluctuation efficiently.
Example
Simplex for LRA:
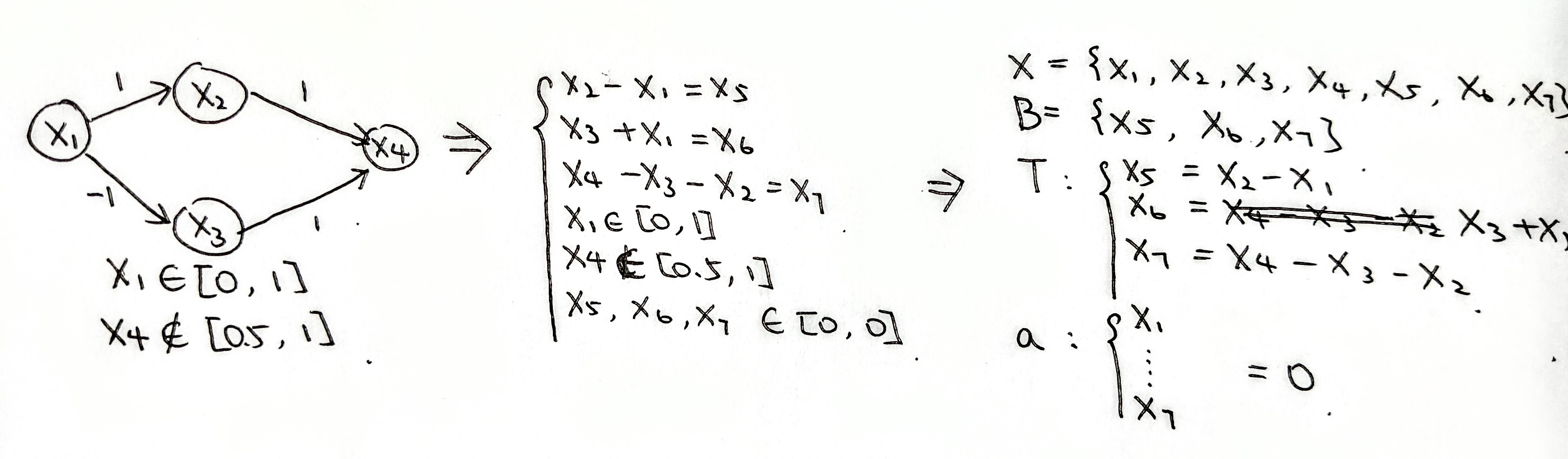

Reluplex: